Разлохмаченные мысли о линейной перспективе.

О линейной (научной, ренессансной и пр.) перспективе написано довольно-таки много. Так что, при должном желании, можно с лёгкостью найти достаточно материала для изучения.
Впрочем, подавляющее большинство этих материалов не слишком полезно как для практикующих, так и для теоретизирующих фотографов. Поскольку посвящено не столько объяснению общих принципов, сколько обучению практическим приёмам построения перспективных изображений.
Такой перекос в практику вполне естественен. Ведь линейная перспектива - это, в теории, очень простое геометрическое построение (не сложнее, допустим, аксонометрии), а вот практическое исполнение этого простого построения не столь уж просто, и к тому же тесно связано с рядом условностей (ограничений), зависящих как от решаемых задач, так и от несовершенства метода.
Фотографу же вся эта практика ни к чему, поскольку все построения за него выполняет фотоаппарат. Однако, даже поверхностное знакомство с общим принципом не помешает, и может объяснить некоторые... э... "феномены".

Итак, что же такое линейная перспектива?
Это способ проецирования трёхмерных пространственных форм на двумерную плоскую (или иную) поверхность, при котором все проецирующие лучи (прямые) проходят через одну общую и неподвижную точку (центр проекций, "точку зрения", "нодальную точку" объектива).
И в общем-то всё...
По сути, единственность центра проекции - это единственное строгое условие перспективного проецирования, остальные же, так называемые, "законы перспективы" из этого условия вытекают.
Т/е весь набор понятий, связанных с перспективой (мнимое и предметное пространство, точки стояния, схода, удаления и пр.) относятся к практике перспективных построений и облегчают не столько понимание, сколько создание перспективных изображений при заданных условиях (например, при заданном положении наблюдателя). Поэтому, не стоит считать, допустим, перпендикулярность картины предметной плоскости (земле) - "законом перспективы". Это - всего лишь заданное условие (например, для изображения вертикалей вертикальными).
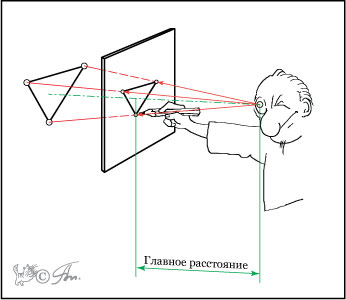
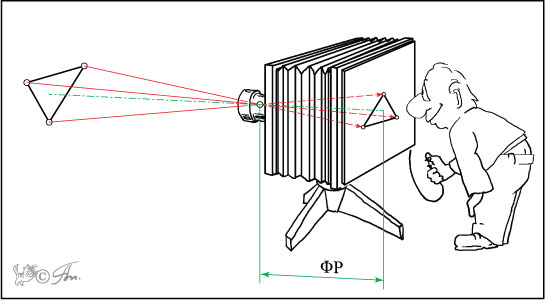
Впрочем, некоторые из этих понятий аналогичны и даже идентичны фотографическим (точнее, оптическим). Так например, "точка зрения" (центр проекции) = "нодальная точка" объектива, "главный луч зрения" = оптическая ось объектива, а "главное расстояние" (по главному лучу, от точки зрения до картины) = ФР.

***

Далее..
Общеизвестно, что перспективное изображение создаёт иллюзию глубины.
За счёт чего? За счёт искажения масштабов (ближний-больше, дальний-меньше, а на самом деле одинаковы).
Почему искажаются масштабы? Потому что проективные лучи втыкаются в картину под разными углами (чем дальше объект, тем меньше угол). Т/е вся "глубина" существует за счёт разницы углов.
Очевидно, что поскольку центр един и неподвижен, то зависимость угла от удаления отнюдь не постоянна. И чем дальше объекты от центра проекции (или чем меньше поле зрения), тем удаление всё меньше и меньше изменяет угол.
Т/е, по мере уменьшения угла зрения, так же уменьшается и заметность удаления. А соответственно и "глубина".

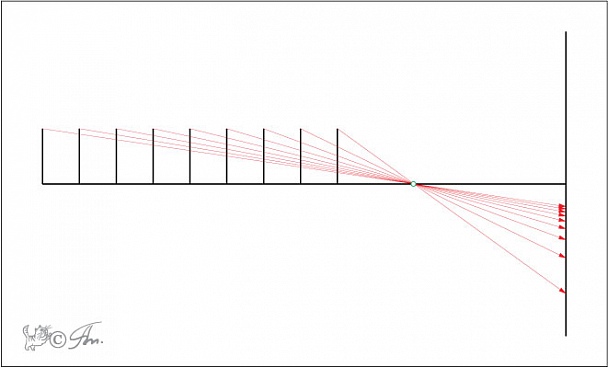
Собственно, именно это неотъемлемое свойство центрального проецирования и наблюдается при изменении ФР.

По сути, отношение ФР к формату определяют угол зрения системы, который, в свою очередь, определяет некоторый конус, "вырезаемый" из пространства. И если центр проекции неизменен, то остаются неизменными и все отношения масштабов. Какой бы конус не вырезался.


***
Впрочем, как я уже сказал, с перспективой связаны и некоторые ограничения, которые, в частности, обусловлены тем, что результат центрального проецирования не столь уж полно соответствует видимой глазом картине.

Даже если абстрагироваться от "двуглазости" и "мозговой постобработки", то неплохо бы вспомнить, что картинка-то проецируется отнюдь не на плоскость. Т/е, геометрически правильная перспективная проекция на плоскость будет соответствовать "сетчаточной" только до тех пор, пока разница между длиной дуги не слишком отличается от её (дуги) высоты (в среднем +/-15°).
Так что, хотя, теоретически, и можно построить плоское перспективное изображение любой точки почти-что 180°-го поля, однако "естественными" будут восприниматься лишь небольшая часть этих изображений, ограниченная этими самыми +/-15°(в среднем)*. И кстати, учебники по перспективе вообще не рассматривают построений для углов более +/-26,5° (что соответствует отношению 1/1 диагонали к ФР), поскольку перспективные эффекты при этом заведомо "неестественны".
Впрочем, при разглядывании излишне широкоугольного изображения непосредственно из центра проекции, перспектива может показаться и вполне естественной, за счёт центрального проецирования плоской картины на криволинейную "сетчаточную" поверхность (типа "свёртывания" краёв).
***
Вполне очевидно, что проецирование трёхмерного предмета на двумерную плоскость невозможно без искажений. Искажаются формы, искажаются размеры.
Рельсы, там, внезапно™ сходятся, и/или... э... носы у моделей вытягиваются...
Но поскольку метод перспективного проецирования свойственен человеческому глазу, то некоторые из этих искажений человек принимает как "естественные", и даже частенько искажениями-то не считает. Отсюда и рассуждения об "искажённой" перспективе шириков или длиннофокусников, хотя метод проецирования остался тем же, а иногда и с тем же центром проекции.

На самом же деле, по мере удаления (уменьшения угла зрения, увеличения ФР) происходит некое перераспределение ошибок. Уменьшается ошибка масштабов (искажения отношения размеров), но растёт ошибка глубины**. Что вполне естественно, поскольку, чем перпендикулярнее проективные лучи к плоскости картины, тем проекция ближе к ортогональной*** (с её точным соотношением размеров и полным отсутствием "глубины").

Впрочем, не стоит считать всё сказанное призывом выбрасывать на ближайшую помойку извращённую "неестественную" оптику...
Художникам давно уже известны эти проективные тараканы, и они давно уже пользуются искажениями в качестве изобразительного средства.
Хотя и с переменным успехом...
Да конечно, классические портретисты традиционно жертвуют глубиной ради сохранения масштабов, но на самом деле, выбор тараканов только на вашей совести...
---------------------------------------------------------------------------------------------
* Кстати, и так наз. "поле наилучшего зрения" ограничено ~30°.
** Раушенбах называл этот феномен линейной перспективы "законом сохранения искажений", и считал суммарное искажение ~ 55%.
*** Точнее к параллельной, в более общем случае неперпендикулярности картины к оптической оси (главному лучу зрения).

---

p.s. Я вполне сознательно ограничился геометрией, и не стал затрагивать проблем восприятия. Хотя несомненно, что особенности человеческого восприятия оказывают сильнейшее воздействие на видимую естественность перспективного изображения.
Однако, восприятие - это слишком обширная тема, чтобы сводить её к двум-трём лозунгам (хотя я вполне готов об этом потреньдеть™).
К тому же, фотоаппарат проецирует пространство именно в линейной перспективе (при отсутствии дисторсии разумеется).